MK,MK体育,MK体育官网,MK体育app,MK体育网址“大单元视角下的一元一次方程行程问题结构化活动设计与实践”主题，创新构建“概念内化—模型生成—实践赋能”三位一体结构化活动范式。以校园运动会这一贴近学生生活的主题情景为教学切入点，设计从基础相遇问题起步，经，最终至跨领域问题迁移应用的梯度化探究任务链，引导学生深度参与方程模型构建与应用的全过程，以此突破传统方程教学中知识零散化、应用能力浅层化、素养培育边缘化等现实瓶颈，全面提升学生的数学建模、逻辑推演等核心素养以及应对复杂现实问题的关键能力

　　在基础教育数学课程标准指引下，针对“大单元视角下的一元一次方程行程问题结构化设计与实践”主题，我系统整合教学内容并细化为课时学习目标，聚焦行程问题的概念理解、模型构建、解法掌握及思维培养四大核心要素。通过构建从基础相遇到复杂追及、最终实现跨领域迁移的结构化活动链，结合学情与资源灵活调整教学策略，以情境化、探究式活动激发学生主动学习，深度落实课程标准，促进学生数学核心素养的全面提升与行程问题的深度掌握。

　　怎么学：以问题驱动开启行程方程学习，采用独立钻研与小组合作探究。在行程情境中巧设未知数，借助图表梳理路程、速度、时间关系，构建方程框架。深挖典型行程场景等量关系，参与实践调整策略，强化对概念的理解，提升解决实际行程问题的能力。

　　学生已掌握有理数运算、一元一次方程解法及行程问题的算术解法，并具备相关生活经验，能直观感受行程问题。

　　2、新知内容分析本单元围绕大单元视角下的一元一次方程行程问题结构化活动展开，深入探究其在行程问题中的应用，助力学生从算术思维向代数思维转变，掌握标准解法与建模方法，为后续学习奠基。

　　3、学习能力分析七年级学生运用一元一次方程解决行程问题时，虽有一定基础运算与逻辑思维能力，且问题贴近生活能激发其兴趣，但存在概念理解不透彻、方程构建困难、计算符号易错、忽视检验步骤及思维转换障碍等问题。为此，需强化概念阐释、系统培养方程构建技巧、严格规范求解检验流程，并专项训练思维转换能力，以有效提升学生学习效能。

　　4、学习障碍的突破策略学生在学习用一元一次方程解决行程问题时，常遇概念理解不透彻、方程构建困难、求解检验能力不足及思维转换障碍等挑战。对此，可通过强化概念直观教学、借助典型例题练习培养方程构建能力、加强求解检验训练、采用类比归纳促进思维转换、实施分层教学因材施教及鼓励合作学习交流启发等策略，有效突破难点，提升学生数学素养与解题能力。

　　通过一元一次方程大单元的学习，学生将全面理解方程的基本概念与解法，能够运用所学知识从实际问题中抽象出数学模型，并通过合并同类项、移项等方法求解方程，进而提升解决实际问题的能力，强化数学建模与应用意识的培养，为数学学习的持续进阶奠定稳固基石。

　　（1）通过观察、分析典型行程问题，如相遇与追及场景，精准提炼速度、时间、路程等关键数量关系，抽象出一元一次方程在行程问题中的本质特征，并能用数学语言清晰阐述其概念。

　　本课时评价任务聚焦一元一次方程在行程问题中的运用，依循新课标，借助典型案例引导学生历经问题抽象、变量设定、方程构建与求解验证等关键环节，着重培育数学建模、数学抽象、逻辑推理等核心素养。通过表现性、过程性、成果性、反思性多元评价手段，精准评估核心素养发展状况，及时反馈学习成效，深化知识理解应用，推动学科核心素养的有效达成。

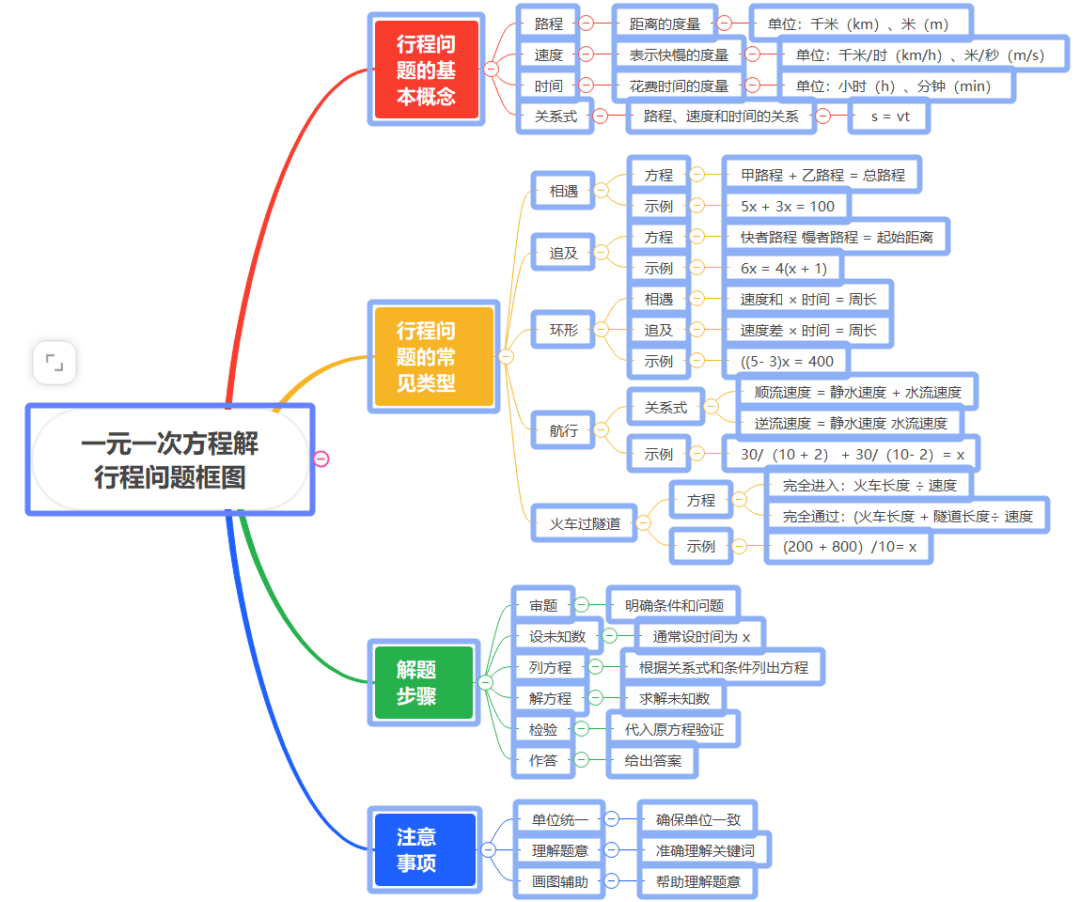
　　【设计意图】此行程知识结构图通过结构化活动设计，精准提炼一元一次方程在行程问题中的应用要点，将多种行程场景与方程解法紧密相连，形成清晰知识脉络。它遵循大单元教学理念，为学生构建系统学习框架，涵盖基本概念、常见类型、解题步骤及注意事项，助力学生全面掌握行程问题解决方法，提升数学素养。

　　以速度、时间、路程为核心要素构建行程问题思维导图，融入相遇与追及等问题类型，清晰呈现各要素间及问题类型与核心要素的关联逻辑。

　　两地相距150公里，甲、乙相向而行，速度分别为5公里/小时和10公里/小时。设相遇时间为t小时，请列出方程？

　　小明从A点出发，小华从距A点100米的B点出发，两人同向同时跑。小明速度8公里/小时，小华6公里/小时。设小明追上小华需t小时，请列出方程？（注意单位）

　　例1：校园运动会“长跑对决”中，小明和小强从相距84km的赛道两端同时出发相向而跑，半小时后相遇。已知小明速度比小强快20km/h。求小强的速度？

　　引导：方程为0.5x+0.5(x−20)=84，两种方法本质相同，培养灵活性。

　　问题6：若赛道长度为d km，速度差为k km/h，方程如何调整？ 引导：方程变为0.5x+0.5(x+k)=d，深化方程建模能力。

　　【设计意图】“校运探秘1”以结构化活动为载体，依托“校园运动会相遇问题”情境，遵循“建模→推理→验证→迁移”的思维进阶链，将“速度-时间-路程”关系与一元一次方程应用深度融合。活动引导学生从实际情境中抽象数学关系、建立方程模型，在参数化拓展与多解法对比中深化模型理解，强化逻辑推理与数学抽象能力；同时紧扣单元核心任务，将问题解决方法迁移至制作规划、消费决策等生活场景，构建系统化知识体系，形成可迁移的结构化思维工具，实现核心素养培育与知识迁移应用的有机统一。

　　例2：校园运动会，甲、乙两队在操场追逐。甲队从距起点 100 米的“一号营地”出发，速度每秒 1.2 米；乙队从距起点 300 米的“二号营地”出发，速度每秒 0.8 米。多长时间后，甲队在途中追上乙队？请你先试着用列算式的方法解决。

　　引导：设甲队追上乙队所需时间为t秒，甲队位置为100+1.2t米，乙队位置为300+0.8t米。

　　引导：设甲队初始位置为a米，速度为v 1 米/秒；乙队初始位置为b米，速度为v 2 米/秒。则方程为a+v1· t=b+v 2· t，培养灵活性与迁移能力。

　　【设计意图】“校运探秘2”延续“校运探秘1”的结构化设计理念，依托校园运动会追及情境，深化一元一次方程在行程问题中的应用。通过“抽象建模→逻辑推理→验证反思→拓展迁移”路径，以层次化问题链驱动探究，展示算式与方程解法，培养灵活思维。参数化拓展强化模型普适性，紧扣单元任务，关联前序活动，形成系统化知识体系，全面提升核心素养与问题解决能力。

　　例3：在校运会期间，校车作为交通纽带，穿梭于王家庄、翠湖（主会场）、青山与绿水之间，接送参赛师生。已知青山距翠湖50km，绿水距翠湖70km，校车匀速行驶，并记录下途经王家庄、青山、绿水三地的时间如表。请求出王家庄距翠湖的路程有多远?

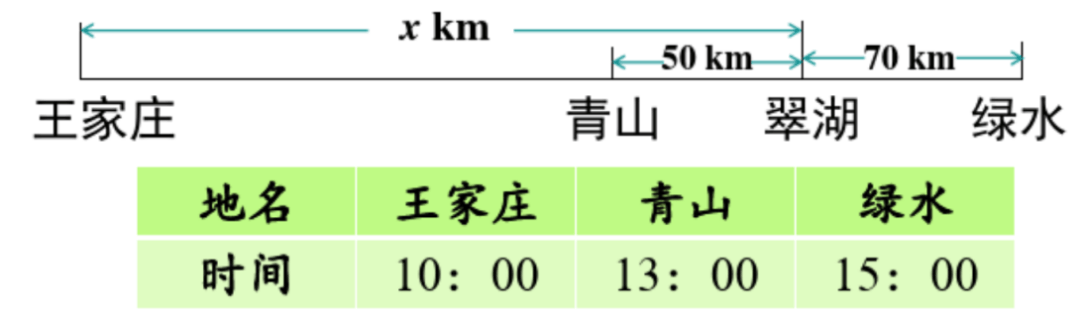
　　情境描述：校车在校运会期间穿梭于王家庄、翠湖、青山与绿水之间，接送师生。

　　问题提出：已知青山距翠湖50km，绿水距翠湖70km，校车行驶时间节点，求王家庄到翠湖的路程。

　　抽象问题：将实际问题抽象为数学问题，设王家庄到翠湖的路程为x km，利用校车匀速行驶的条件建立方程。

　　建立方程：根据校车从王家庄到青山和绿水的时间关系，利用速度相等原理，建立方程(x - 50) / 3 = (x + 70) / 5。

　　逻辑分析：通过速度相等原理，检查答案是否符合校车行驶时间、路程与速度的关系。

　　【设计意图】“校运探秘3”在“校运探秘2”的结构化设计理念基础上进一步拓展，以校车行驶情境深化一元一次方程的应用。通过情境导入、建模、求解、验证及反思，不仅掌握路程求解方法，引导学生全程参与，深度思考，实现了数学知识与核心素养的双重提升。

　　（1）在校园运动会上，李明和刘伟在600米的环形跑道上跑步。李明每分钟跑190米，刘伟每分钟跑210米。两人同时从起点反向出发。

　　（2）在校园运动会的长跑训练中，田径队的“客车组”和“卡车组”同时从起点A出发，沿同一跑道匀速奔跑。已知：客车组速度为70米/分钟，卡车组速度为60米/分钟， 客车组比卡车组早1分钟到达终点B。问：起点A到终点B的跑道长度是多少米？

　　【设计意图】“校运探秘4”紧扣新课程标准，构建教学评一致性结构化模块。借助校园运动会情境中的“环形相遇”与“直线追及”问题，驱动学生完整经历建模、推理、验证过程，强化核心素养，实现教、学、评有机统一，促进知识整合与素养发展，彰显数学教学的实践与育人价值。

　　必做：（1）校园运动会水上项目中，学生们组织划船比赛。一艘船从甲码头顺水划到乙码头用时2小时，逆水返回用时2.5小时。已知水流速度为3千米/小时，求该船在静水中的平均速度？

　　选做：（2）在校运动会期间，一列运送运动员的火车匀速通过一条300米长的隧道，耗时20秒。隧道顶部有一盏灯，灯光照射在火车上的时间为10秒。

　　【设计意图】本次作业设计基于校园运动会情境，以结构化理念构建行程问题解决框架。必做题通过顺水逆水问题夯实行程基础，选做题借火车过隧道拓展物体长度与运动关系，培育高阶思维。注重即时评价反馈，预设解析助纠错。遵循大单元理念，融入核心素养，完善行程问题类型理解，促进思维发展。

　　本次教学紧密贴合2022版新课程标准理念，以校园运动会为鲜活的大主题情境，精心开展了《大单元视角下的一元一次方程行程问题结构化活动设计与实践》。在结构化活动设计中，巧妙地将行程问题的各类基本情境，如相遇追及、顺水逆水等，编织成一条逻辑清晰、环环相扣的问题解决链条。教学过程中，着力引导学生从丰富具体的运动情境中提炼出数学模型，熟练运用一元一次方程攻克实际难题，从而深化对知识间内在关联与严谨逻辑结构的理解。与此同时，依托多样化的评价任务，实现了对学生学习成效的即时、精准反馈，有力推动了学生思维的进阶发展。回顾反思本次教学，结构化活动设计与校园运动会情境的深度融合成效显著，不仅极大地增强了学生的数学应用意识，更全方位提升了学生的数学核心素养。展望未来，将持续深耕结构化活动设计，进一步挖掘情境教学的独特育人价值，为学生的数学素养提升与全面发展注入更强动力。

　　吴小红，华师教育研究院研究员，高级教师，县学科带头人、县优秀教师；先后担任过小学信息技术、英语、数学和初中数学等教学工作；主讲的小学信息技术和小学英语优质课分别获市、省一等奖；曾参加省教科院小学英语课题研究，获取的教学经验在全省大会上交流与推广；撰写英语案例获省特等奖，单元教学案例共5篇约3万字已编入《湖北省小学英语教学应用指导手册》并推广使用，20多篇论文获国、省、市级一、二等奖，其中两篇发表在《中国信息技术教育》杂志上。返回搜狐，查看更多